|
今天介绍一种工程上常用的前馈+PI控制器。 先看看前馈控制的基本定义。
前馈控制的好处是直接控制无滞后,可以提高系统的响应速率,但是需要比较准确地知道被控对象模型和系统特性。而反馈控制的优点是不需要知道被控对象的模型即可实现比较准确的控制,但是需要偏差发生之后才能进行调节,具有滞后性。 所以,理论上把前馈和反馈结合起来,既能实现较高的控制精度,也能提高系统响应速度,下面仿真说明。 直流电机模型我们需要一个被控对象模型,这里选择一个12V直流电机作为被控对象(前面也有文章使用过)。直流电机的数学表达式为: U=I*R+Ke*φ*w+L*dI/dt Te=Kt*φ*I Te-TL=J*dw/dt+B*w 基于上述表达式,直流电机的Simulink模型可表示为下图所示,这里与以前电机模型有区别的地方是电机外界负载用一个与转速正相关的Map表示,即TL=0.0005*n,电机每增加1000rpm的转速,外界负载扭矩加大0.5N。 这里做的目的就是为了设置一个电机特性,为后面的前馈控制做准备。 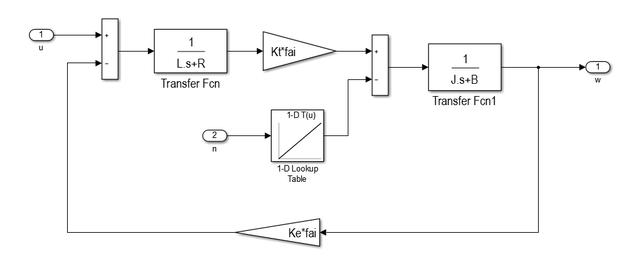 PI控制效果先把之前的积分分离PI控制器拿过来,看看对这个电机的控制效果,PI控制器模型如下图。 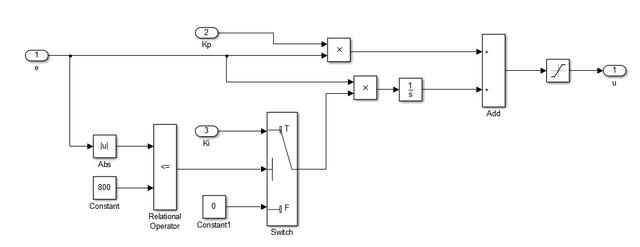 给定一个2000rpm的目标转速,调整一下PI参数尽量达到无超调的最好效果,结果如下:系统无超调,达到稳定状态的时间大约1.8s。 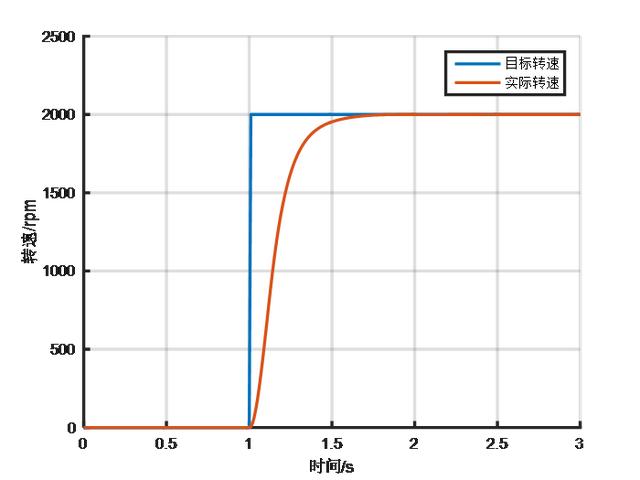 前馈+PI控制效果前馈+PI反馈的控制结构如下图。 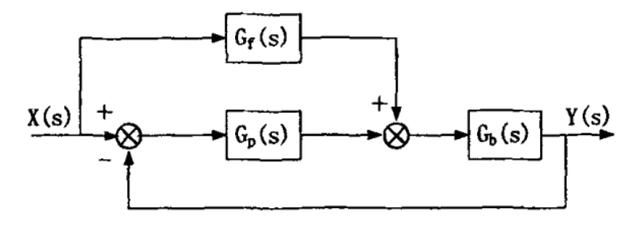 Gb(s)是被控对象,Gp(s)是PI控制器,Gf(s)是前馈控制器。 考虑在控制器加上一个前馈量,怎么加? 其实就会要找到控制量与被控量之间的关系,即u=f(n)。 前面已经假定电机外界负载特性为TL=0.0005*n,如果想控制电机稳定在某一转速,那么必须让电机出固定的扭矩来平衡外界负载扭矩和自身负载扭矩,即电机扭矩为 Te=0.0005*n+B*w I=Te/Kt/φ U=I*R+Ke*φ*w,其中w=n*pi/30 所以,可以计算出来 U= 0.00267*n 在PI控制器中增加一个前馈控制量0.00267*n。 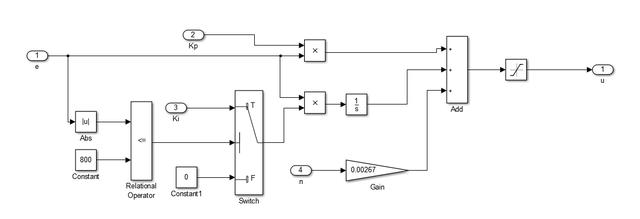 给定一个2000rpm的目标转速,调整一下PI参数尽量达到无超调的最好效果,结果如下:系统无超调,达到稳定状态的时间大约1.55s,达到稳定的响应时间会比单独的PI控制更快。 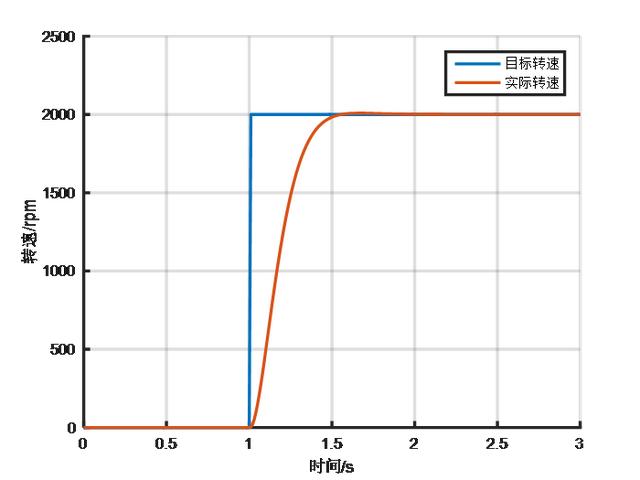 使用前馈后,一般可以适当减小PI参数,以获得更好的综合控制效果。 工程应用实际在工程应用中,被控对象的模型或外界干扰不一定能完全准确获得,可能会存在一定的偏差。这种情况一般怎么处理? 还是以上面的仿真为例,假设我们获取的外界负载特性偏大或偏小,则前馈量也会出现一定偏差,系统响应曲线会如下图。前馈量偏大,会出现较大的超调,系统稳定时间变长,但响应会变快;前馈量偏小,则不会出现超调,但响应速率会稍慢。 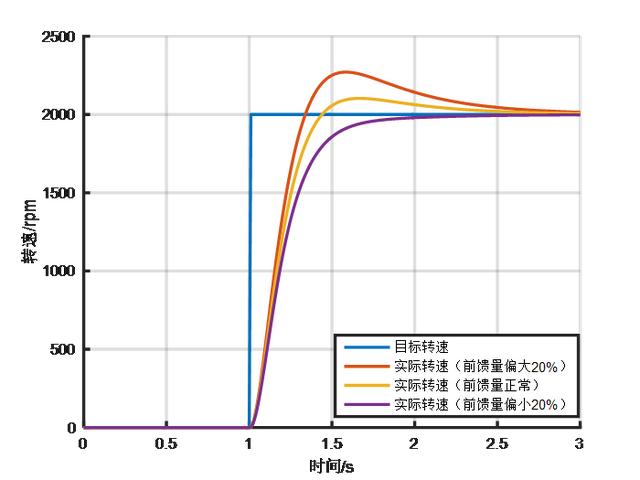 一般地,对于响应时间没有太多要求的,且系统特性获取会存在偏差时,可以适当减小前馈量,如仅保留80%前馈量,通过反馈进行修正,可以保证系统响应无超调,比较平顺。 汽车上有很多这种前馈+PI反馈控制的应用实例,如增程汽车的增程器控制(把发动机的实际扭矩作为前馈量给到发电机进行转速控制),蠕行控制(把坡道对应的重力分量作为前馈量给到控制器进行扭矩控制)等等。 总结来说,前馈控制用于确定基本的控制量级别,来得快且直接,反馈控制用于误差修正,能确保稳和准,两者配合则可获得各自优点。如果前馈控制做得足够准的话,反馈控制是可以去掉的,但是实际很少这样做,因为系统是不断变化的,需要反馈保证稳定性。 以上,对前馈+PI控制器进行简单介绍,更多经验需要大家在工程中慢慢发现。 后面有机会可以结合控制理论和工程实践,来分析各种控制器的特点。 文章来源【新能源汽车控制】版权归原作者所有 |
